Definitions:
The moment of inertia (Mass MOI or Rotational Inertia) of a rigid body is a quantity that determines the amount of torque needed for a desired angular acceleration about a rotational axis.
The MOI of an object about rotational axis is the measure of an object resistance to change in the object’s angular acceleration due to action of couple or torque.
The MOI of a rigid body can be obtained by imaging the body being subdivided into numbers of particles. The mass of each particle is then multiplied by its squared distance from the axis and then it sums up these products for all the particles in the body.
Moment of Inertia units:
Moment of Inertia SI Unit – kg.m2
Area moment of inertia- mm4 or in4
Mass moment of inertia- kg.m2 or ft.lb. s2
Dimensional Formula- M1L2T0
Factors affecting MOI:
It is scalar quantity because its value about a given axis of rotation remains unchanged by reversing its direction of rotation about that axis.
Greater the moment of inertia of a body, greater is the couple (Torque) required to produce a given angular acceleration.
MOI is depending upon how an object mass is distributed with respect to its axis of rotation.
A body does not have a single Moment of Inertia but potentially an infinite number of Moment of Inertia, one for every different an axis of rotation.
If MOI is small it is relatively easy to rotate angularly. Therefore, with less moment of inertia accelerate faster.
It is much harder to rotate an object with greater mass with the same radius. Similarly, it is much harder to rotate an object with same mass and larger radius.
Moment of Inertia Formula:
In the case of translators motion, value of inertia depends only on the mass of the body. The kinetic energy in such motion depends on the mass and linear velocity of the body.
When a body rotates about an axis of rotation, the kinetic energy of rotation is determined not only by its mass and angular velocity but also depends upon the position of the axis about which it rotates and distribution of mass about this axis of rotation.
Let’s assume a body of mass m rotating about an axis of rotation AB with angular velocity ὠ. All its particles have the same angular velocity but particles are at different distances from the axis AB, their linear velocities are different.
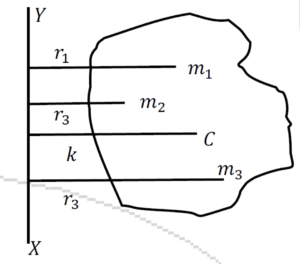
Hence, we get
$$KE=\frac12m_1{v_1^2}_+\frac12m_2v_2^2+…$$
$$KE=\frac12m_1r_1^2{\omega_1^2}_+\frac12m_2r_2^2{\omega^2}_2+…$$
$$KE=\frac12(\sum_-mr^2)\omega^2\\KE=\frac12I\omega^2$$
Here, I denote the MOI.
MOI of general bodies:
1.Rod
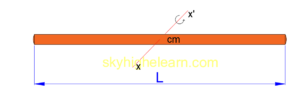
a) A uniform rod of negligible thickness, the moment of inertia at the centre of is,
Where, mass of the rod is M and length is L.
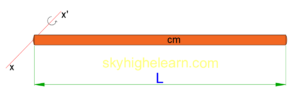
b) Similarly by using parallel axis theorem the MOI of rod about the rod end can be,
2.Cylinder
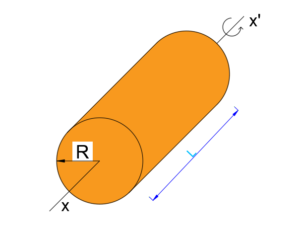
a)Axis of rotation passing through the center of solid cylinder and perpendicular to its plane.
where, R is the radius of the cylinder and M is the mass of the cylinder.
b)MOI of cylinder about its diameter.
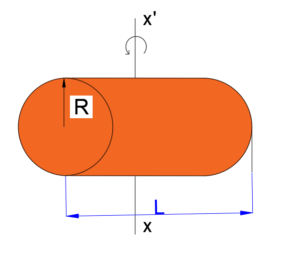
c)Thin walled cylinder about central axis.
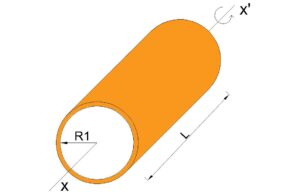
D)Similarly, Thick walled cylinder about central axis.
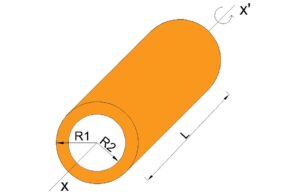
$$I=\frac12M(R_1^2+R_2^2)$$
3.Sphere
a)MOI of solid sphere about centre.
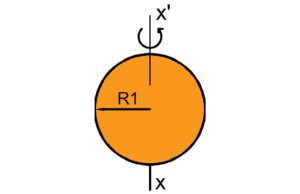
b)MOI of thin hollow sphere.
$$I=\frac23MR^2$$
You also like to read:
1.Mechanical design engineer interview questions and answers for freshers.
2.Mechanical engineering interview questions and answers for freshers.
3.Top 30 hr interview questions and answers for freshers all jobs.
4.How to select right bearing for your application.


